The first thing to remember when calculating gear ratios is that we compare two distances with each other. If we compare a circle with the radius of 100 to a circle with the radius of 50 we get a 0.5 ratio. The same is true if we compare the perimeter of both circles.
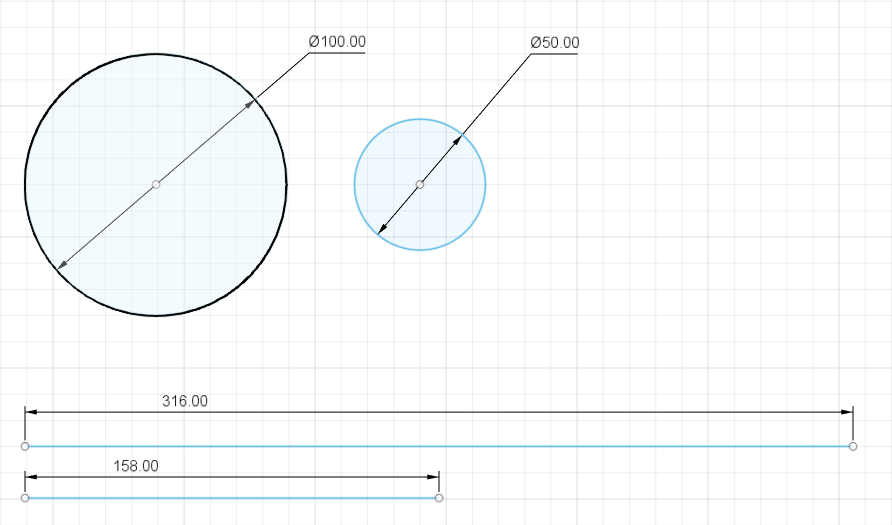
The second important constant to remember is that for intermeshing gears to work the distance between the teeth as well as the teeth size needs to be the same on both gears.
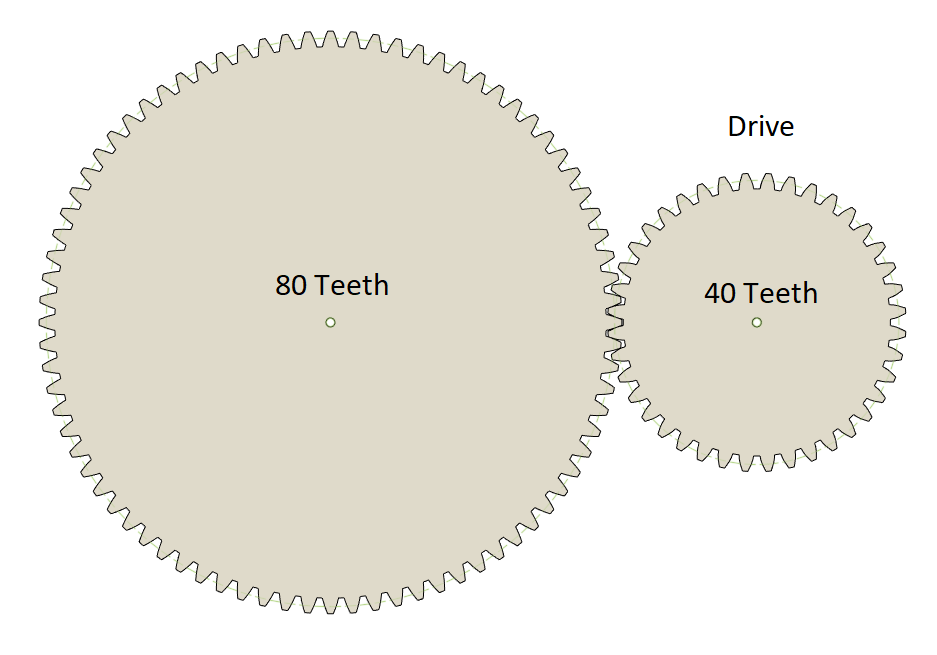
In the following picture we have two gears that engage with each other. Two or more gears that engage with each other are called a gear train. The driver gear that starts the motion has 40 teeth and the driven gear has 80 teeth. To get the gear ratio you have to divide the driven gear teeth (80) by the drive gear teeth (40). In this example the calculation looks like this:
\[Ratio = {driven \over drive } = {80 \over 40 } = {2 \over 1 } = 2 : 1\]
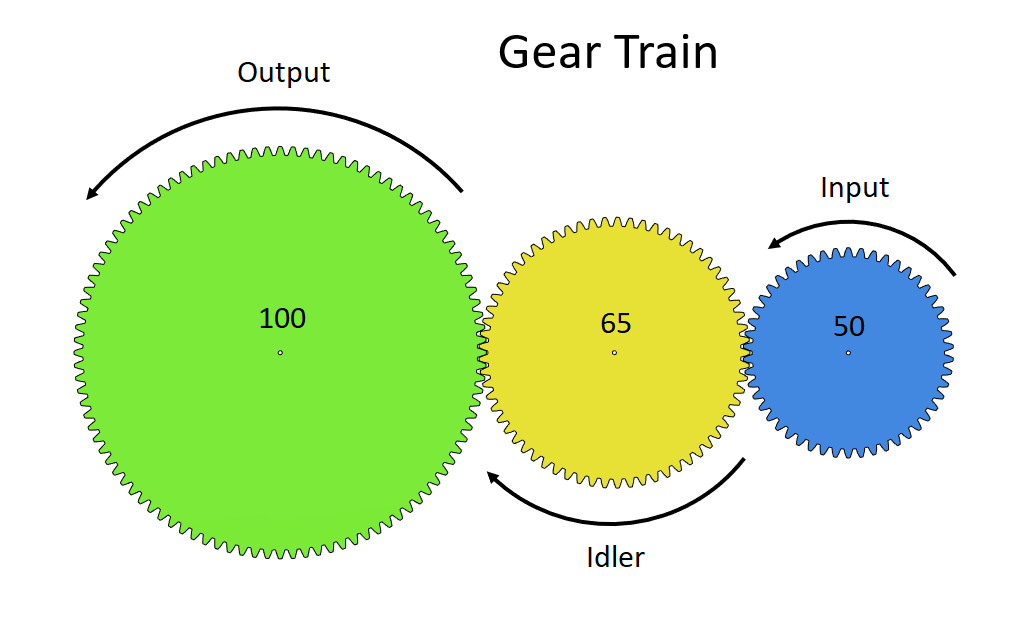
If you have more than two gears in a gear train you need to identify the driver and the driven gear - In the following picture they are called input and output. The gears between the driver and the driven are called idler. Idler gears are usually used for changing the gear direction or to overcome some space limitations that prevent you from attaching your output gear to your input gear. The idler gears can be ignored in the ratio calculation. Use the same calculation as above to get your ratio:
\[Ratio = {output \over input } = {100 \over 50 } = {2 \over 1 } = 2 : 1\]
To calculate the ratio of compound gears you have to split them up in gear trains first and calculate them as described above. For the following example we get out two ratio calculations:
\[Ratio_{(P+G)} = {green \over pink } = {80 \over 40 } = {2 \over 1 } = 2 : 1\] \[Ratio_{(B+O)} = {orange \over blue } = {120 \over 20 } = {6 \over 1 } = 6 : 1\]
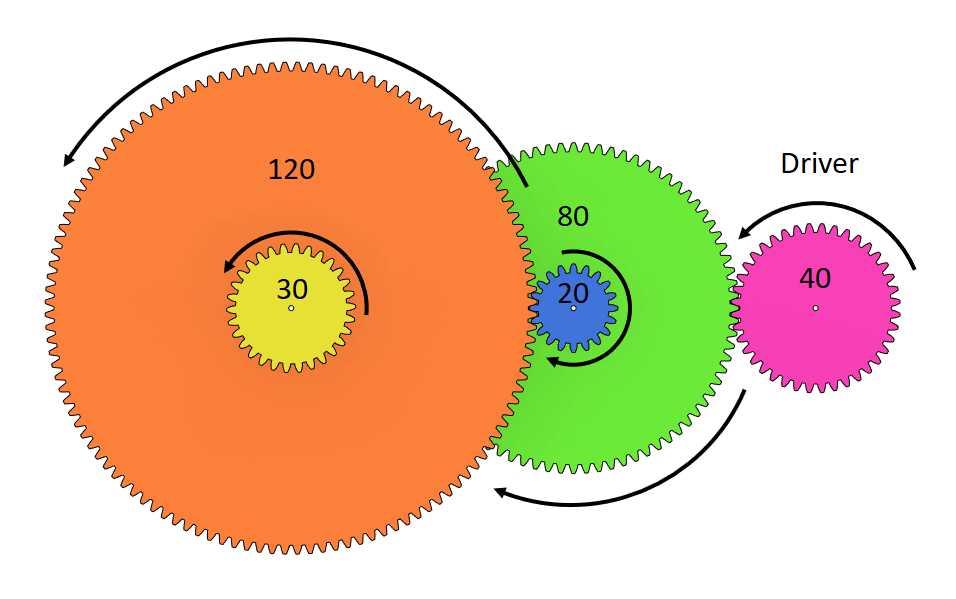
To get the end result for the compound gear example we multiply our calculations from the last step:
\[Ratio_{(sum)} = {green \over pink } * {orange \over blue } = {2 \over 1 } * {6 \over 1 } = {12 \over 1 } = 12 : 1\]